
 || разделы:: || разделы:: | |
 || поиск по сайту:: || поиск по сайту:: | |
 || реклама:: || реклама:: | |
 || новости почтой:: || новости почтой:: | |
 Популярные статьи Популярные статьи |
|
 Hot 5 Stories Hot 5 Stories |
|
 || рекомендуем:: || рекомендуем:: |
|
|  |
Поиск по графу
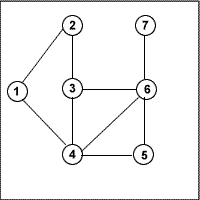 Предлагаю всем желающим решить следующую задачку: необходимо написать программу поиска пути на графе от заданного начального узла графа до заданного целевого узла. Пример графа вы видите на рисунке. Хотя это лишь для наглядности - желательно чтобы алгоритм поиска не зависел от структуры графа и не был привязан к конкретным узлам (начальному и конечному).
Предлагаю всем желающим решить следующую задачку: необходимо написать программу поиска пути на графе от заданного начального узла графа до заданного целевого узла. Пример графа вы видите на рисунке. Хотя это лишь для наглядности - желательно чтобы алгоритм поиска не зависел от структуры графа и не был привязан к конкретным узлам (начальному и конечному).
Свой вариант, написанный на Perl, я привожу ниже, а попробовать ее в действии вы можете здесь: //webscript.ru/cgi-bin/intel/intel.cgi
Поиск не должен быть оптимальным, скорейшим и т.д. - такой задачи пока не стоит, надо просто отыскать верное решение.
Кроме того, данная статья - эксперимент, эксперимент над посетителями WebScript.Ru, который заключается в проверке необходимости подобных материалов.. нужно вам это или нет? Все-таки мы отдаем себе отчет в том, что данная задачка представляет скорее теоретический интерес нежели практический, хотя :) на практике некоторые идеи применить можно.
Кто сказал, что все просто?
На первый взгляд, задача кажется весьма простой (а еще проще она смотрится, если нарисовать дерево графа, но это на бумажке), весьма интересно посмотреть на другие варианты достижения поставленной задачи… А как эту задачу решить средствами PHP? ;)
Пояснения к моему решению:
Граф задан в виде хеша массивов:
%point=(1 => [4, 2],
2 => [1, 3],
3 => [4, 2, 6],
4 => [1, 5, 3],
5 => [4, 6],
6 => [5, 4, 3, 7],
7 => [6]);
Где ключ - это узел, а соответствующее ему значение-массив, список узлов связанных с ним. По-моему, весьма разумное представление графа, кроме того, такую структуру весьма несложно генерировать, и таким образом задавать различные структуры графа (это к слову о графонезависимости). Как задавать структуру графа - дело ваше, главное, чтобы это было честно (ведь можно задать структуру дерева графа, а это облегчит задачу).
Как осуществляется поиск? Объясню на пальцах: допустим нам надо найти путь от 1-го узла к 5-му.
1. Закидываем начальный узел в массив пути @ariadna
Название массива не случайно, Ариадна - дочь царя острова Крит, которая дала герою Тезею клубок ниток и он таким образом вышел из Лабиринта Минотавра. И существует даже выражение "Нить Ариадны", т.е. путеводная нить. Наш массив @ariadna полностью соответствует названию, сюда мы будем заносить все узлы, которые прошли, а само решение (если оно существует) рано или поздно окажется в этом массиве.
2. Минуя различные бюрократические проволочки мы попадаем в подпрограмму sub check_point, которая берет последний узел из массива @ariadna, получает список связанных с ним узлов @list=@{$point{$path}}; и начинает их проверять на "пригодность". В чем заключается пригодность?
Если узел из списка оказывается тем из которого мы только что пришли, если этот узел мы уже приходили или если узел тупиковый, то он не пригоден - он выкидывается из списка @list, и для нашего узла (а пока мы рассматриваем узел 1), мы записываем новую 'карту состояний', вернее новый список связанных с ним узлов без учета "непригодного" узла. Если в процессе проверки выясняется, что перед нами новый узел, который мы еще не проходили, то он заносится в массив @ariadna, далее, он выкидывается из карты состояний узла проверки (сейчас это 1-й узел) и мы отправляемся исследовать новый узел.
Т.е. в нашем случае, мы получили список узлов, связанных с 1-м (это 4-й и 2-й), берем первый попавшийся (4-й), он оказывается пригодным ( его еще нет в @ariadna), тогда мы из карты 1-го узла его выкидываем ( теперь у нас считается, что 1-й узел связан лишь со 2-м, который мы еще не проверяли), мы закидываем 4-й узел в @ariadna и отправляемся исследовать его.
3. 4-й узел у нас связан с 1-м, 5-м и 3-м. Берем то, что попалось под руку, т.е. 1-й. Так.. а мы тут уже были, 1-й содержится в @ariadna (проверку уникальности осуществляет подпрограмма sub check_uniq), выкидываем 1-й узел из карты 4-го узла; говорим всем и каждому, что опыт не удался (возвращаем return 0; до подпрограммы sub deep_search), а потом отправляемся проверять узел 5-й (теперь он в карте 4-го узла первый), ого! Да мы 5-й и ищем! Все, уходим отсюда! Только предварительно не забудем 5-й узел добавить в массив @ariadna:
if ($point==$finish){
push (@ariadna, $point);
return 'end';
}
А если бы в списке 4-го узла пятого не оказалось? Тогда бы мы проверили 3-й, перешли бы в него и т.д. А если бы 4-й узел был тупиковым? Тогда, убедившись в его тупиковости (карта состояний - пустой массив), мы бы поднялись на уровень вверх, выкинув его из @ariadna:
pop @ariadna;
@{$point{$path}}=@list;
return 0;
Т.е. мы бы вернулись в 1-й узел, а в его карте остался лишь 2-й (4-й мы выкинули, перед тем как отправились к нему в гости). Вот так и ползем: проверяем. Если все глухо, отходим на шаг назад и проверяем то, что еще не проверили.
Данный вариант поиска называется "Поиск в глубину". Если решение существует, то мы до него рано или поздно доползем, плохо то, что мы идем до упора по одному пути, пока не упремся лбом в стену... а ответ может быть совсем рядом, надо было лишь вначале свернуть в другую сторону. Есть другой способ - "Поиск в ширину", т.е. мы не идем до упора, а заглядываем во все закоулки, если не видим ответа, то заглядываем в более глубокие закоулки (но во все!) - иногда, так можно найти ответ быстрее.. но об этом в следующий раз!
Хотелось бы услышать ваше мнение по поводу таких задачек - нужно ли публиковать подобное на webscript.ru или нет? Это :) эксперимент.
Сама программа:
#!/usr/bin/perl -w
#Слепой поиск в глубину
#Автор:Green Kakadu (gnezdo@webscript.ru)
#-----------------------------------------
use vars '%point', '%bid', '$start', '$finish', '@ariadna';
#Задаем граф - ключ узел,
#значения в массиве - узлы, которые с ним связаны
%point=(1 => [4, 2],
2 => [1, 3],
3 => [4, 2, 6],
4 => [1, 5, 3],
5 => [4, 6],
6 => [5, 4, 3, 7],
7 => [6]);
&main;
sub main {
#--------------------------------------
$start||=1;
$finish||=7;
&deep_search;
}
sub deep_search {
#---------------------------------------
my $res;
push (@ariadna, $start);
my $i;
#Проверяем до тех пор не найдем результат, или проверим все пути
until($res){
$i++;
print $i,': ', @ariadna, "\n";#вывод рез-тов каждого шага
$res=&deep_search_routing;#провер-ка очередного узла
unless (@ariadna){last;}#выход из цикла если проверены все пути
}
if ($res){$my_print=join("->", @ariadna);}
else {$my_print = "К сожалению, ничего не найдено!";}
$my_print .=" Кол-во проверок: $i\n";
print $my_print;
exit;
}
sub deep_search_routing {
#----------------------------------------
my $search=&check_point($ariadna[$#ariadna]);#'расширяем' узел
if ($search){return 'Find!';}#true если есть ответ!
else{return 0;}#false - продолжаем поиск
}
sub check_point {
#-----------------------------------------
my $path=shift;
#расширяем узел и смотрим, что еще не проверено
my @list=@{$point{$path}};
unless(@list){
pop @ariadna;#тупик! сделаем шаг назад!
@{$point{$path}}=@list;
return 0;
}
foreach my $point(@{$point{$path}}){
if ($point==$finish){
#добавляем рассматриваемый узел
push (@ariadna, $point);
return 'end';#Уря! Найдено!
}
elsif ($point == $path){
#если узел тот, из которого мы только что пришли...
#
#удаляем узел из списка целей для рассматрив. узла
shift @list;
#сохраняем урезанный список целей для данного узла
@{$point{$path}}=@list;
unless(@list){
pop @ariadna;#тупик! сделаем шаг назад!
return 0;#ищем дальше!
}
}
elsif (&check_uniq(@ariadna, $point)){
#если тут мы еще не бывали...
#удаляем узел из списка целей для рассматрив. узла
shift @list;
push (@ariadna, $point);#делаем шаг вперед!
#сохраняем урезанный список целей для данного узла
@{$point{$path}}=@list;
return 0;
}
else {
#если тут мы были...
shift @list;
if (@list){@{$point{$path}}=@list;}
else {
pop @ariadna;#тупик! сделаем шаг назад!
#сохраняем урезанный список целей для данного узла
@{$point{$path}}=@list;
}
return 0;
}
}
return 0;
}
sub check_uniq {
#----------------------------------------
#Проходили мы здесь или еще нет? Надо проверить...
#
my @list=@_;
my %uniq=();
foreach my $elm(@list){
if ($uniq{$elm}){return 0;}
$uniq{$elm}++;
}
return 1;
}
|
|
::::: St.BURn пишет 12.11.2001 @ 13:05 | |
Почитай теорию графов - полезная вещь в решении этой задачи... Я бы помог, но перл еще не освои... Помнится решал я обход графа, вернее поиск в графе в ширину и глубину, но на паскале... Чтобы долго не мучаться почитай про матрицы смежности и инцидентности... Будут вопросы пиши...
|
|
::::: Гоша пишет 04.12.2001 @ 16:22 | |
Вот если бы вместо этой игрушки показали, как найти оптимальный и скорейший путь... А так-то какой от скрипта толк? Впрочем, думаю, что давно уже такие скрипты написаны.
|
|
::::: Антон пишет 09.12.2001 @ 14:26 | |
Данная задача разрешена.
я не пробовал ее писать на перловке или на пхп но алгоритм поиска пути в графе стандартный и реализовать его на любом языке программирования не сложно.
так что читайте теорию графов (теория оптимизации) "поиск кратчайшего пути в графе"
|
|
::::: Влад пишет 13.12.2001 @ 16:22 | |
А по моему очень полезный пример. А то где не ткнись сплошь и рядом гостевые книги и счетчики:(. А этот пример может и надуманый но сознание расширяет:)!
|
|
::::: Sergey пишет 25.12.2001 @ 10:23 | |
Действительно, надо читать дискретку. Там много всего интересного. Ну а алгоритмы поиска пути со всякими разными критериями уже давно известны (Краскала, Дейкстры и др.). Так что не понимаю смысла этой статьи.
|
|
::::: Shadow пишет 02.01.2002 @ 20:42 | |
Мило... по моему интересней было бы рассмотреть
пример поиска минимальной ДНФ, для заданного
корректно синтаксического условия. Для сложного
поиска на сервере.
Regards, 12.34.16.60
|
|
::::: Serhi пишет 22.02.2002 @ 02:25 | |
Хочу высказаться по данному вопросу. Я не знаком c Perl и PHP , но в свое
время передо мной стояла такая задача.Нужно было написать программу поиска пути
по графу. Причем у меня были очень жесткие ограничения по времени поиска,
а размер графа был около двухсот тысяч !!! вершин. Так вот , хочу сказать -
вся теория графов , имеющаяся на данный момент имеет один серьезный недостаток.
Она вся написана для небольших графов. Для 10-100 вершин она работает нормально
, но уже для тысячи время поиска будет долгим.Пришлось отказаться от существующей теории и искать полностью свое решение , адаптированное под огромные графы. Я сидел над этим очень долго
но все таки создал алгоритм удовлетворивший поставленным условиям.Двухсоттысячный граф он обрабатывал за 0.6 секунды (максимум), на 400-ом процессоре . Он реализован на C++. Если кого то это интересует - пишите.
P.S. В интернете есть программы поиска по большим графам . Их цена просто ошарашивает.
|
|
::::: Alec пишет 25.02.2002 @ 14:00 | |
Привет! Будь проще!
%TTT = ( 0=> [0,1,0,0,1],
1=> [1,0,1,1,0],
2=> [0,1,0,1,0],
3=> [0,1,1,0,0],
4=> [1,0,0,0,0]
);
#это таблица связности вершин графа: 1 на пересечении - есть дуга, 0-нет
$Fe = 4; # вершина-цель
%PATHS=(); # тут хранятся пути
$Paths_Count = 1; #"бюрокрастические" изыски :-))
print"
Поиск путей к кластеру #$Fe\n
Таблица связности:
0 1 2 3 4
";
foreach $c (sort keys %TTT) {
print "$c ", join ' ',map { $_ == 0 ? '-' : '+'} @{$TTT{$c}};
print "\n";
}
print "\n\n";
&deep(3); # deep (откуда_искать)
#печать находок
foreach $p (sort keys %PATHS) {
printf "%-5d : %s\n",$p,join ('->',reverse @{$PATHS{$p}});
}
sub deep
{ my $cluster = shift;
my @path = @_;
my @conn;
my $cc,$i;
#список вершин, куда можно ходить (нас там не было!)
for ($i = 0; $i < 5; $i++) {
push @conn,$i if ($TTT{$cluster}[$i] && !IsClusterAlreadyInPath($i,@path));
}
foreach $cc (@conn)
{ if ($cc eq $Fe) {
$PATHS{$Paths_Count++} = [$cc,$cluster,@path];
return;
}
deep($cc,($cluster,@path));
}
}
sub IsClusterAlreadyInPath {
my $cluster = shift;
my @path = @_;
my $temp = join '-',('',@path);
return $temp =~ /-$cluster/;
}
|
 |
|
::::: IxIon пишет 30.01.2003 @ 16:22 | |
Да... Любим мы изобретать велосипеды...
Все уже придумано..
Алгоримт Флойда для небольших графов, тама рекурсия...
Алгоритм Дейстры для всех...
Читаем теорию графов и радемся...
Реализовать плевое дело
|
|
::::: Xmen пишет 29.03.2003 @ 13:18 | |
что вы ристали??? Этот пример для раскрутки мозгов и посмотреть кто и как решит данную проблемму, если не хотите отвечать на задачу, так и не пишите, а то достали блин, все такие умные, тоьлко вот решения я отвас не видел, одни лиш указания... Читайте то читайте сё... Темболее эта задачка написана для тех людей, которые начинают изучать и что бы показать возможно языка (или языков)... Блин прям как малые дети.....
ПРОГРАММИСТ НЕ ПРОГРАММИСТ ЕСЛИ НЕ НАПИШЕТ СВОЮ ПРОГРАММУ... Ведь гордость каждого программиста это своя написаная программа, а не взятая чужая....
|
|
::::: Стирч пишет 14.08.2003 @ 13:47 | |
А Такое пишется на лиспе в 10 строчек. и писать такое надо на лиспе.
|
|
::::: MACTEP пишет 28.08.2003 @ 18:57 | |
А интересно - кто напишет наиболее короткую (по числу операторов) программу на Perl для этого ? Вот тогда такая задача и ее решение было бы интересным.
|
|
::::: Druid пишет 24.09.2003 @ 18:45 | |
Подобные задачи интересны чисто теоретически. И я думаю многие нарешались их еще в институтах или другим местах. Твою задачу я решал в 9 классе на время и на Паскале.
А потомм подобную, но сложнее решал на вступительных экзаменах в институт. Там кстати за вывод как у тебя на http://webscript.ru/cgi-bin/intel/intel.cgi (вся цепочка построения пути) мне снизили оценку до четырех. Хотя все 5 задач решались в течении полуторачасов на !бумажке!...
хе-хе
Прошу прощения, что не в тему.
Модератор, если посчитаешь флудом - удаляй.
|
|
::::: Druid пишет 24.09.2003 @ 19:00 | |
И еще, если сделаешь динамическую генерацию графа, то будет интересннее.
|
|
::::: SplashX пишет 28.09.2003 @ 22:55 | |
твой алгоритм хоть и работает , но бредово напимер путь межжду 1 и 1 это 1->4->1 бред , а до 3
:1 -> 4 -> 5 -> 6 -> 3 у меня есть свой на Delphiне он ищет оптимальный путь , пока всего 50 строк
|
А вот кто нибудь подскажет где можно найти примеры
реализации для больших графов ??
заранее благодарю
|
|
::::: nik пишет 10.02.2004 @ 10:25 | |
А как реализовать на перле поиск в глубину и ширину?
|
|
::::: пишет 24.07.2004 @ 14:24 | |
|  |

